1. 버블 정렬(bubble sort)
- 정렬(sorting): 데이터를 정해진 순서대로 나열하는 것
- 두 인접한 데이터를 비교해서 앞에 있는 데이터가 뒤에 있는 데이터보다 크면 자리를 바꾸는 정렬 알고리즘

1-1. 버블 정렬 알고리즘 구현하기
- 데이터가 4개일 때(예: data_list=[1, 9, 3, 2])
- 1차 로직 적용
- 1과 9 비교, 자리바꿈 X [1, 9, 3, 2]
- 9와 3 비교, 자리바꿈 O [1, 3, 9, 2]
- 9와 2 비교, 자리바꿈 O [1, 3, 2, 9]
- 2차 로직 적용
- 1과 3 비교, 자리바꿈 X [1, 3, 2, 9]
- 3과 2 비교, 자리바꿈 O [1, 2, 3, 9]
- 3과 9 비교, 자리바꿈 X [1, 2, 3, 9]
- 3차 로직 적용
- 1과 2 비교, 자리바꿈 X [1, 2, 3, 9]
- 2와 3 비교, 자리바꿈 X [1, 2, 3, 9]
- 3과 9 비교, 자리바꿈 X [1, 2, 3, 9]
- 1차 로직 적용
- 특징
- n개의 리스트가 있는 경우 최대 n-1번이 로직을 적용한다.
- 로직을 한 번 적용할 때마다 가장 큰 숫자가 뒤에서부터 하나씩 결정된다.
- 로직 적용 시 데이터의 교환이 이루어지지 않았다면 이미 정렬된 상태이므로 로직을 반복 적용할 필요가 없기에 경우에 따라 일찍 끝날 수도 있다.
- 코드 구현
2. 삽입 정렬(insertion sort)
- 두 번째 원소부터 앞에 있는 정렬된 부분과 역방향으로 값을 비교하며 자신의 자리를 찾아감
- 더 작은 값이 나오면 그 자리에 삽입하고 나머지 원소들은 한 칸씩 뒤로 밀림
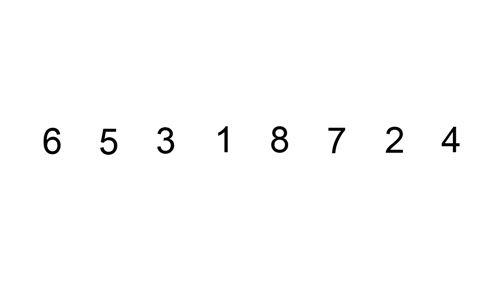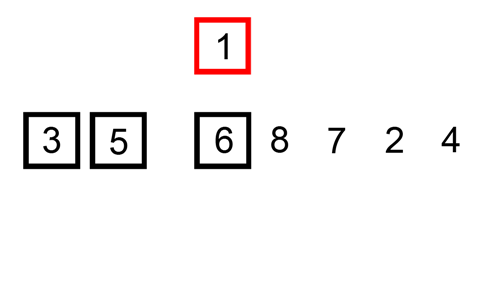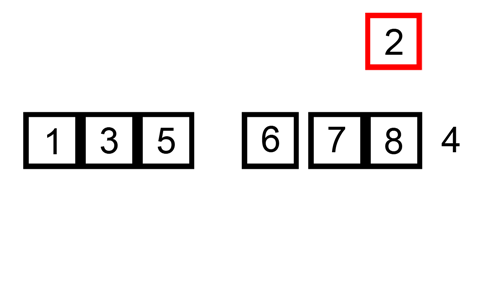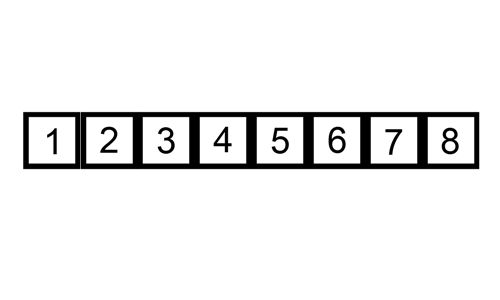
2-1. 삽입 정렬 알고리즘 구현하기
- 데이터가 네 개일 때(예: data_list = [9, 3, 2, 5])
- 처음 실행하면 key 값은 9, 인덱스(0) -1은 0보다 작으므로 끝: [9, 3, 2, 5]
- 두 번째 실행 key 값은 3, 9보다 3이 작으므로 자리 바꾸고 끝: [3, 9, 2, 5]
- 세 번째 실행 key 값은 2, 9보다 2가 작으므로 자리 바꾸고, 3보다 2가 작으므로 자리 바꾸고 끝: [2, 3, 9, 5]
- 네 번째 실행 key 값은 5, 9보다 5가 작으므로 자리 바꾸고, 3보다 5가 크므로 끝: [2, 3, 5, 9]
def insertion_sort(data):
for index in range(len(data) - 1):
for index2 in range(index + 1, 0, -1):
if data[index2] < data[index2 - 1]:
data[index2], data[index2 - 1] = data[index2 - 1], data[index2]
else:
break
return dataimport random
data_list = random.sample(range(100), 20)
print(data_list)
print(insertion_sort(data_list))
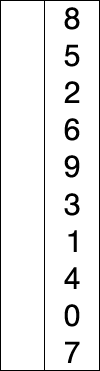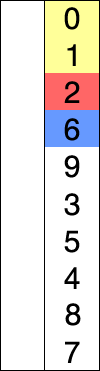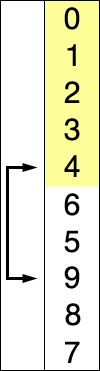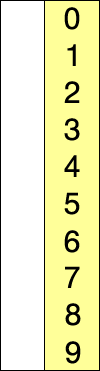
3. 선택 정렬(selection sort)
- 주어진 데이터 중 최솟값을 찾고 해당 최솟값을 데이터 맨 앞으로 이동시킴
- 위의 과정을 반복함
3-1. 선택 정렬 알고리즘 구현하기
- 데이터가 두 개일 때 (예: data_list = [9, 1])
- data_list[0] > data_list[1] 이므로 data_list[0] 값과 data_list[1] 값을 교환
- 데이터가 세 개일 때 (예: data_list = [9, 1, 7])
- 처음 실행하면 [1, 9, 7]
- 두 번째 실행하면 [1, 7, 9]
- 데이터가 네 개일 때 (예: data_list = [9, 3, 2, 1])
- 처음 실행하면 [1, 3, 2, 9]
- 두 번째 실행하면 [1, 2, 3, 9]
- 세 번째 실행하면 변화 없음
def selection_sort(data):
for stand in range(len(data) - 1):
lowest = stand
for index in range(stand + 1, len(data)):
if data[lowest] > data[index]:
lowest = index
data[lowest], data[stand] = data[stand], data[lowest]
return dataimport random
data_list = random.sample(range(100), 20)
print(data_list)
print(selection_sort(data_list))
<알고리즘 구현 과정 작성>
1. 버블 정렬
# 처음 작성한 코드
# 결과물 버블 정렬이 이루어지지 않음
def bubble1(data):
for index in range(len(data)):
if data[index] > data[index + 1]:
data[index] = data[index + 1]
data[index + 1] = data[index]
return data
else:
return data
data = [1, 9, 3, 2]
bubble1(data)
1단계 첨삭
- range(len(data)) 수정하기
- range(len(data))라고 작성 시 리스트 데이터 길이 만큼 반복 횟수가 설정된다. 버블 정렬의 경우 n개의 리스트 있을 때 최대 n-1번의 로직을 적용해야 하기 때문에 range(len(data)-1)로 수정해야 한다.
- return 동작 이해하기
- return data 시행 시 data가 반환되고 함수가 끝난다. 따라서 현재 data = [1, 9, 3, 2]에서 for 문에 의해 index == 0인 경우 else가 시행되고 값이 반환된 후 함수의 동작은 끝이나게 되므로 for 문이 내가 원하던 것처럼 반복 시행되지 않았다.
- if문 인덱스 자리 바꾸는 코드 한 줄로 작성할 수 있다.
- a, b = c, d 일 때 a = c, b = d
def bubble2(data):
for i in range(len(data)-1):
for idx in range(0, len(data)-1 -i):
if data[idx] > data[idx + 1]:
data[idx], data[idx + 1] = data[idx + 1], data[idx]
# print(data)
return data
data = [1, 9, 3, 2]
bubble2(data)
2단계 첨삭
- for문 과정을 print 값으로 살펴봤을 때 버블 정렬이 잘 이루어진 걸 확인할 수 있었다. 나아가서 flag 변수를 활용해 for문을 세우는 연습을 해 봐야겠다.
- flag 변수: 조건에 따라 True, False 값을 넣어주는 Boolean형 변수로서 특정 동작을 수행할지 말지 결정하거나 약속된 신호를 남기기 위한 용도로 쓰인다.
# 최종 완성 코드
def bubble3(data):
for i in range(len(data)-1):
flag = False
for idx in range(0, len(data)-1 -i):
if data[idx] > data[idx + 1]:
data[idx], data[idx + 1] = data[idx + 1], data[idx]
flag = True
if flag == False:
break
return data
data = [1, 9, 3, 2]
bubble3(data)
2. 삽입 정렬
# 처음 작성한 코드
def insertion1(data):
for i in range(0, len(data)):
for idx in range(0, i):
if data[i] < data[idx]:
data[i], data[idx] = data[idx], data[i]
# print(data)
return data
data = [9, 3, 2, 5]
insertion1(data)
첨삭
- 결과는 정렬이 되었지만 print로 과정을 보면 삽입 정렬이 이루어지지 않았다.
- key 값이 2일 때 [3, 9, 2, 5] -> [3, 2, 9, 5] -> [2, 3, 9, 5] 순으로 정렬 즉, 뒤에서 앞으로 가는 순으로 자리 바꿈 동작이 일어나야 하지만 지금 작성한 코드는 [3, 9, 2, 5] -> [2, 9, 3, 5] -> [2, 3, 9, 5] 순으로 정렬 즉, 앞에서 뒤로 가는 순으로 자리 바꿈 동작이 일어난다.
- 중첩 for문에서 range(0, i)를 수정하여 자리 바꿈 동작 순서를 다시 생각해 보자...
# 최종 완성 코드
def insertion2(data):
for i in range(0, len(data)):
for idx in range(i, 0, -1):
if data[idx] < data[idx-1]:
data[idx], data[idx-1] = data[idx-1], data[idx]
print(data)
else:
break
return data
data = [9, 3, 2, 5]
insertion2(data)
3. 선택 정렬
# 처음 작성한 코드
def selection1(data):
for i in range(0, len(data)-1):
lowest = data[i]
# 최솟값 찾기
for idx in range(i+1, len(data)):
if lowest > data[idx]:
lowest = data[idx]
# print(f'최솟값: {lowest}')
# 최솟값을 앞으로 위치 시키기
lowest, data[i] = data[i], lowest
# print(f'인덱스 {i}의 값: {data[i]}')
# print(data)
return data
data = [9, 3, 2, 1]
selection1(data)
첨삭
- lowest, data[i] = data[i], lowest 수정
- 최솟값을 앞으로 위치 시킬 때 인덱스에 있던 기존 값과 자리를 바꾸는 동작이 일어나야 하는데 최솟값을 인덱스 값에 입력하여 기존 값을 덮어 쓰는 동작이 일어났다... [9, 3, 2, 1] -> [1, 3, 2, 9] 가 되어야 함.
- lowest = data[i] 수정
- 최솟값을 덮어쓰니까 for 문에서 최솟값이 고정되어 정렬값이 [1, 1, 1, 1] 됨... "lowest, data[i] = data[i], lowest 수정"보다 우선적으로 lowest를 지정할 때의 좋은 방법이 없을지 고안해 봐야겠다.
- 해결법: lowest = data[i] 처럼 최솟값을 아예 값으로 지정하지 말고 최솟값 포인터 역할을 할 수 있도록 lowest = i 처럼 코드를 수정하면 된다!
# 최종 완성 코드
def selection2(data):
for i in range(0, len(data)-1):
# 최솟값 찾기
lowest = i # 최솟값 포인터
for idx in range(lowest + 1, len(data)):
if data[lowest] > data[idx]:
lowest = idx
# 최솟값을 앞으로 위치 시키기
data[i], data[lowest] = data[lowest], data[i]
print(data)
return data
data = [9, 3, 2, 1]
selection2(data)
모르는 부분 및 깨달은 부분
- 모르는 부분: 여전히 모르겠는 부분은 함수 안에서 중첩 for 문을 사용했을 때 내가 원하는 만큼 반복을 시행하고 싶은데 (1) 어떻게 작성해야 return 없이 전체 범위 반복을 시행할 수 있는지 (2) 어떻게 작성해야 조건을 만족할 때 하나의 조건문만 벗어나고 다른 조건문으로 넘어갈 수 있는지 (1), (2) 이 둘을 빠르게 생각해내기 어렵다. 아무래도 파이썬 기초 문법이 확실하게 정립되지 않은 상태인 것 같으니 다시 한번 함수 부분과 반복문 부분을 깊게 복습해야겠다는 생각이 든다...
- 깨달은 부분: 알고리즘 구현 코드 작성할 때 알고리즘 로직을 머릿속으로만 생각하고 작성하니까 막히는 부분도 많고 결과도 제대로 나오지 않았다. 그런데 하나의 데이터를 예시로 들어서 로직을 구체적으로 쪼개가며 손으로 직접 묘사한 뒤 코드를 작성했더니 구현하기가 훨씬 수월했다. 귀찮고 어렵더라도 코드 짜기 전에 알고리즘 로직을 생각하고 짜는 것이 구현에 도움이 많이 되고, 이해하기 어려웠던 로직도 보다 잘 이해된다는 것을 몸소 느꼈다.
'파이썬 > 파이썬 자료구조와 알고리즘' 카테고리의 다른 글
| 파이썬 자료구조 (7) 힙 (0) | 2024.10.21 |
|---|---|
| 파이썬 자료구조 (6) 트리 (0) | 2024.10.17 |
| 파이썬 자료구조 (5) 해시 테이블 (1) | 2024.10.16 |
| 파이썬 자료구조 (4) 더블링크드리스트 (0) | 2024.10.16 |
| 파이썬 자료구조 (3) 링크드리스트 (0) | 2024.10.16 |

